這是學習多元線性回歸的實作第三篇
繼上一篇提到資料前處理的操作
今天會正式進入回歸的主題

All-In 方法

下面我們開始用regressor 內建函式做多元線性回歸
regressor 是一個擬合好的回歸器
我們呼叫predict() 並帶入測試集(應變量)
會得到一個預測好的結果(自變量)叫y_pred
y_pred 就是預測的各state的營業額(profit)

y_pred = regressor.predict(x_test)

執行後可以用variable explorer 比較y_pred & y_test

從上面結果可以發現
少數公司看起來預測接近實際值
多數公司看起來則是預測與實際有誤差
要注意的是
我們目前用的是All-in 策略
也就是我們幾乎用了所有的應變量來建立模型
但實際上可能某些變數對結果來說影響不是那麼大
現在我們希望優化模型, 將影響不大的變數給去掉
因此接下來嘗試用前幾篇提到的Backward Elimination方法來建模型

Backward Elimination 方法

下圖是多元線性回歸的公式
不過今天要用到的library 不包含constant, 只包含到後面的coeff * X
因此我們需要讓constant 變成 constant * 1
讓公式變成 y = b0 * 1 + b1 * X1 + b2 * X2 + ... + bn * Xn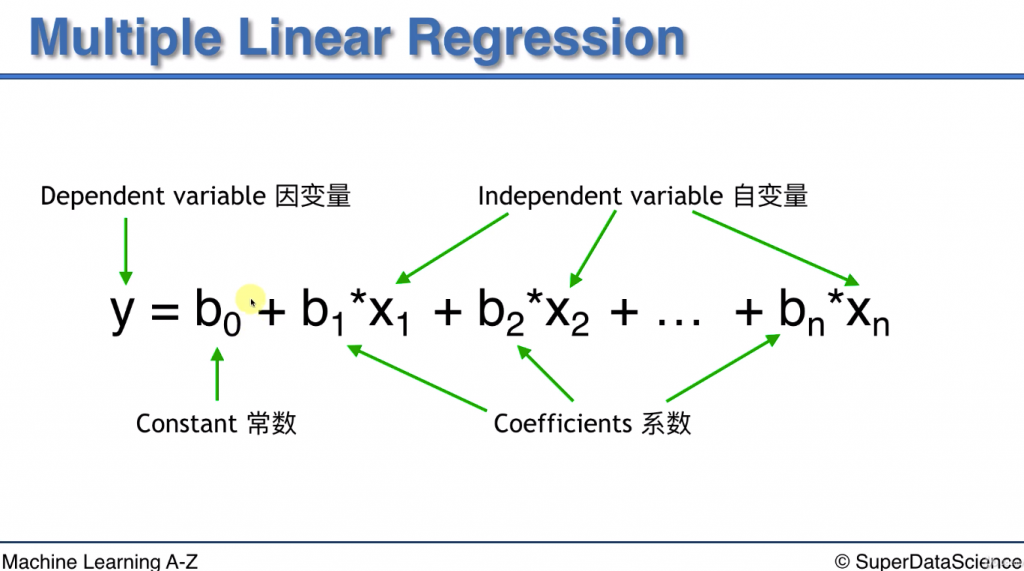

目前x_train 代表的是上面公式裡的X1~Xn
因此我們需要將1也新增到一行資料
而x_train 總共有40行資料
因此需要加入一個40＊1 的矩陣
下面我們用append() 和 ones()來達成
append(arr,values,axis):可用來將矩陣新增一行或一列的方法
arr: target matrix
values: source matrix(目的是將source 新增到target)
axis: 0 = add a new row, 1 = add a new column

ones(shape): 返回一個給定大小的矩陣, 矩陣內容都為1
shape: 新矩陣的行列數

import statsmodels.formula.api as sm
x_train = np.append(arr=np.ones((40,1)), values = x_train, axis = 1

現在我們運行這段程式, 可以看到第一列資料已經全都是我們剛剛append上去的1了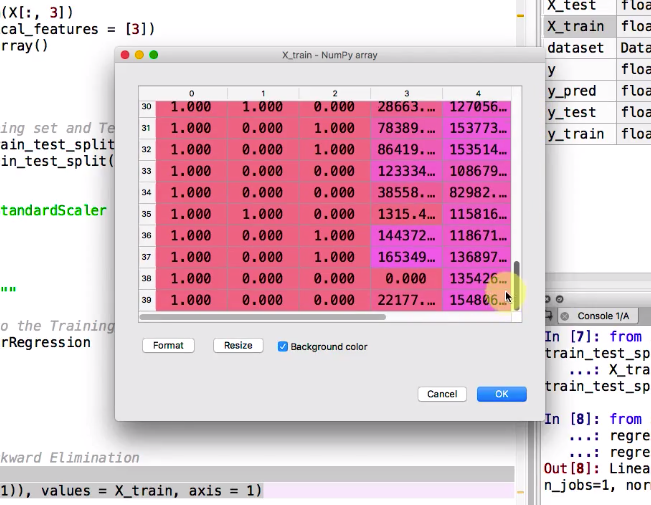

Building the model

以下是課程投影片, 重新複習下backward Elimination 所有步驟

注意:
p-value 越高代表該變數影響力越低, 因此當高過門檻(SL)就將之去除

下面我們用到OLS()和fit()函式來擬合regressor
在用summary 來看regressor 的詳細訊息
OLS(endog,exog)
endog: 應變量
exog: 自變量
fit(): 擬合模型
summary(): 輸出regressor detail information

# round1: (step2)Fit the full model with all possible predictors
x_opt = x_train[:,[0,1,2,3,4,5]]
regressor_OLS = sm.OLS(endog = y_train, exog = x_opt).fit()
# (step3) Check P-value by regressor details
regressor_OLS.summary()

運行這段代碼後可以在console 裡看到regressor details
接著我們看 P>|t| 欄位代表的就是p-value
其中最大的是X2 也就是對應左邊x_opt的黃色框框部分
p-value 已經超過我們設的SL(0.05) 因此代表這個變數影響力不大可以移除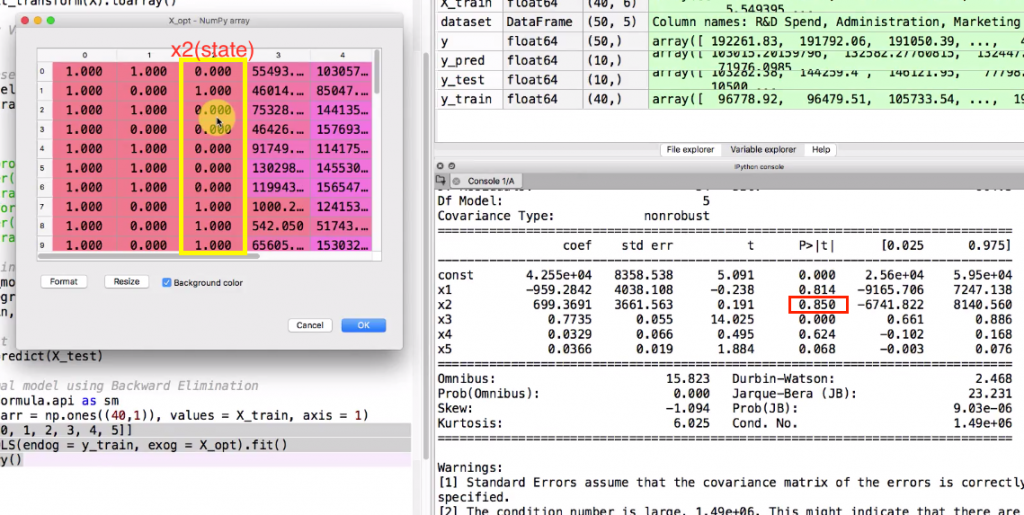

因此接著我們執行第2回合, 將x_train中的column2 拿掉
再重新看一次summary detail
找出最大的p-value 並移除
直到所有的p-value 都 < SL

# round2: (step3)Remove the highest P-value
x_opt = x_train[:,[0,1,3,4,5]]
regressor_OLS = sm.OLS(endog = y_train, exog = x_opt).fit()
regressor_OLS.summary()

過程中會移除的變數順序：
注意：移除兩次state是因為我們先將state 變成兩欄dummy variable
remove 2 (state)
remove 1 (state)
remove 4 (administration)
remove 5 (Marketing) --> 此時p-value 是0.071

最後剩下x1 對應到x_train 裡的第三列 RD spend
代表profit 只和 RD Spend 最強相關
但其實這個方法中ＳＬ的定義很重要, 若ＳＬ變得低一些
很可能就會保留Marketing或是更多變數
因此怎樣選更好看來是一個難題
後面老師會講解到如何用其他方法來判斷線性模型的性能
期待屆時這個問題能得到解答